Дифференциальная форма закона всемирного тяготения в применении к расчету строения Солнечной системы

Ищенко М. Л. 2009

Необходимость расчета деформаций пространства при описании гравитационного взаимодействия

Описание гравитационного взаимодействия в Солнечной системе на основе Закона всемирного тяготения (ЗВТ) было впервые сделано в 1687г. И. Ньютоном (1, с. 170). В формуле классической формы закона использованы физические величины, включающие размерности массы, протяженности и времени, в различных степенях. Исторически сложилось так, что суть природного явления-тяготения изложена на основе законов движения планет И. Кеплера 1609-1611гг (1, с. 173), с помощью физических величин неразрывно связанных с  функцией времени. Дальнейшее уточнение описания гравитационного воздействия проделанное в 1916 г. А. Эйнштейном (2) в Общей теории относительности (ОТО) еще более усилило роль временных параметров. В том числе, для описания гравитационного искривления пространства,  вызванного   массами  вещества, в ОТО  введено  понятие  пространственно-временного континуума.

В то же время, в отдельных случаях гравитационного взаимодействия, давно достигнуто равновесное состояния системы “вещество-пространство”, то есть временные зависимости в равновесном состоянии системы вещество-пространство, не могут иметь большого значения. По этой причине, для Солнечной системы существующий по отдельным оценкам порядка 5 млрд. лет, такая особая роль временных зависимостей кажется сомнительной.  В отсутствии временного фактора, равновесное состояние в системе “вещество-пространство” может достигаться за счет размеров и величины деформации пространства вблизи массы вещества, фактически за счет сил упругости. Поэтому, при расчётах строения Солнечной системы, пространственным характеристикам – деформациям пространства, прогибу, то есть собственно геометрии пространства, следует уделять значительно большее внимание, чем это  предлагалось в ОТО.

Проведенная экспериментальная проверка положений ОТО в Солнечной системе до сих пор не получила однозначного подтверждения (1, с. 377). Совпадение расчётного значения для скорости прецессии Меркурия (43,03″ за  сто лет) с наблюдаемым результатом (43,11 ±0,45″ за столетие) смазывается выявленными отклонениями от шарообразной формы у Солнца, которая заставляет вводить  дополнительную  поправку  в  4″ за  сто  лет.  А  искривление  трассы  световых лучей (на 2″) далёких звезд, при прохождении их вблизи Солнца, хотя так же близко к расчётному значению – (1,7″), но из-за большой (до 10%) погрешности измерений и противоречивости в части данных не может служить доказательством правильности новой теории тяготения, какой считается ОТО.

Более яркие и однозначные примеры прогибов пространства в околосолнечном пространстве можно произвести на основе  законов установленных И. Ньютоном. В классическом виде традиционная запись формулы ЗВТ не позволяет произвести необходимые расчёты деформаций, хотя после небольшого уточнения формулы ЗВТ  такая возможность появляется. При этом, описание равновесного состояния системы “вещество – деформированное пространство”  упрощается и приобретает характер статической зависимости.

О скрытых возможностях закона всемирного тяготеня И. Ньютона в описании деформаций пространства

Классический вид формулы Закона всемирного тяготения (ЗВТ) может иметь ещё и форму дифференциального уравнения. В качестве производных могут быть выбраны как пространственные, так и массовые составляющие. Для составления дифференциальной формы ЗВТ необходимо расположить физические величины, использованные в ЗВТ в виде степенного ряда по размерностям пространственным или массы. Если такой, отранжированный по степеням размерности (длина) ряд физических величин, дополнить производной по кривизне (по дефекту массы) в прилегающем пространстве и представить в виде суммы производных равной нулю,  то получится искомое  дифференциальное уравнение. 

При этом возникает дополнительная возможность решения дифференциального уравнения относительно пространственных производных, дающая возможность описания качественного характера прогиба и расчета численного значений величины прогиба, а решение относительно массовых производных – массы планет. Решения дифференциального уравнения ЗВТ дают возможность получить не только классическую форму ЗВТ, но и дополнительные решения  позволяющие рассчитать  размеры и форму области деформации или массы планет в Солнечной системе.

Кроме того, такой подход позволяет использовать закономерность изменения размерностей задействованных физических величин для составления  дифференциальных уравнений более высоких порядков производных, дающих более точную картину описания гравитационного взаимодействия.

При решении дифференциальных уравнений, используются внутренние балансовые свойства, между размерностями (и числовыми значениями) физических величин у коэффициентов при производных, используемых для описания равновесного состояния системы “вещество – искривленное пространство”. Указанные свойства, проявляются в соблюдении баланса размерностей (числовых значений) при  раскрытии определителей  Раусса и Гурвица (1877г. Routh, Hurwitz), построенных на коэффициентах при производных (3, с. 69). Использование дифференциальных уравнений гарантирует правильное качественное и количественное описание гравитационного взаимодействия с помощью выбранных физических величин.  Необходимо отметить, что решения дифференциальных уравнений для описания гравитационного взаимодействия имеют не только алгебраическую, но и более наглядную геометрическую форму.

Примечание

При составлении дифференциального уравнения предложенным способом для части членов степенного ряда приходится вводить дополнительные множители, с целью приведения размерностей каждого из членов уравнения к одной величине. Полученная сумма производных, при приравнивании её к нулю становится уравнением, решение которого по коэффициентам при производных и самим производным эквивалентно одновременному исследованию функции кривизны иди дефекта массы на поиск экстремального значение соответствующей функции. Корни полученного уравнения дают радиусы орбит и определяют величину кривизны пространства и форму прогиба. А баланс размерностей у коэффициентов при производных (физических величин), привлекаемых в описании гравитационного взаимодействия классическую форму ЗВТ. То есть классический вид ЗВТ, при этом становится  только частным случаем описания гравитационного  взаимодействия.

В   применении  к  Солнечной  системе,  описание  прогибов пространства в сравнительно слабых   гравитационных   полях   даёт   гораздо   более   богатый материал для подтверждения правильности   изложенного   подхода,   чем   ОТО  А. Эйнштейна. Так уже решение относительно производных по пространственным параметрам, даёт спектр значений радиусов орбит планет, а также определяет характер и величины прогибов.

Синтез дифференциальной формы закона всемирного тяготения и ее связь с классической формой закона

Анализ размерностей физических величин в ЗВТ   И.Ньютона показывает, что выбранные физические величины могут быть представлены в виде степенного ряда по размерностям, который формально может рассматриваться как ряд   производных.

$$\begin{equation}
G \\ [L^3M^{-1}T^{-2}]
\tag{1a}\label{1a}
\end{equation}$$

$$\begin{equation}
R^2 \\ [L^2M^0T^0] \tag{1b}\label{1b} \end{equation}$$

$$\begin{equation} F \\ [L^1M^1T^{-1}] \tag{1c}\label{1c} \end{equation}$$

$$\begin{equation} Mm \\ [L^0M^2T^0] \tag{1d}\label{1d} \end{equation}$$

Используем это свойство для записи их в виде дифференциального уравнения. При этом классический вид ЗВТ становится только частным случаем  закона для описания гравитационного взаимодействия. С учётом того факта, что орбиты планет в Солнечной системы близки к круговым, что означает правомочность  равенства продольной и поперечной координат, т.е. при одновременном соблюдении условия  \(х = у\). При этом допущении  прогиб пространства будет осуществляться по координате \(z\) – перпендикулярной плоскости эклиптики, лежащей в плоскости  \(х у\).

$$ G \, Mm \, \frac{\mathrm{d^2}z}{\mathrm{d} x^2} + \frac{m}{t^2} R^2 \frac{\mathrm{d}z}{\mathrm{d}x} + F \, z + \frac{m}{t^2} \int{z\,\mathrm{d}x} = 0 \tag{2}\label{2}$$

Здесь:

• \(\frac{\mathrm{d}z}{\mathrm{d}x}\) производная, пропорциональная прогибу пространства в направлении по оси \(z\) , на участке длиной \(l\) по оси \(х\).
• \(\frac{m}{t^2}\) дополнительный множитель. Его введение вызвано необходимостью приведения к единой размерности для всех членов уравнения. Из приведенных ниже математических выкладок видно, что  введения дополнительного множителя не влияет на результат описания физического явления.

Связь   полученного дифференциального уравнения с классическим видом ЗВТ выявляется при раскрытии определителя Гурвица, построенного на коэффициентах при производных.

$$ \Delta = \begin{bmatrix}\frac{m}{t^2}R^2 & \frac{m}{t^2} \\ G \, Mm & F\end{bmatrix} = \frac{m}{t^2} (R^2F – G \, Mm) = 0 \tag{3}\label{3} $$

Откуда, раскрывая определитель, получим классическую форму ЗВТ

$$ \frac{m}{t^2} (R^2F – G \, Mm) = 0 \tag{3a}\label{3a} $$

$$ F = \frac{G \, Mm}{R^2} \tag{3b}\label{3b} $$

Очевидно, что  наличие дополнительного  множителя  \( \frac{m}{t^2} > 0 \) не влияет на конечный результат проведенного преобразования. Аналогичным дифференциальным  уравнением ЗВТ по дефекту масс может быть уравнение \(\eqref{3c}\):

$$ \frac{1}{r}G \int{m \, \mathrm{d}M} + \frac{1}{t^2}R^2m + F \, r \, \frac{\mathrm{d}m}{\mathrm{d}M} + \frac{R^2}{t^2}(M \, m)\frac{\mathrm{d^2}m}{\mathrm{d}M^2} = 0 \tag{3c}\label{3c}$$

Анализ полученных решений дифференциальной формы закона всемирного тяготения

Полученное дифференциальное уравнение \(\eqref{2}\), которое  является  уравнением третьего порядка производной, которое иногда удобней записывать в операторной форме вида:

$$a_0p^3 + a_1p^2 + a_2p^3 + a_3 = 0 \tag{4}\label{4}$$

Здесь:

• \(a_0 = G \, Mm\)
• \(a_1 = \frac{m}{t^2}R^2\)
• \(a_2 = F \)
• \(a_3 = \frac{m}{t^2}\)
• \(p =\frac{\mathrm{d}z}{\mathrm{d}x}\)
• \(\frac{1}{p} = \int{z \, \mathrm{d}x}\)

Решение уравнения третьего порядка  хорошо известно (4, с. 284, с. 44).  Известно его полное решение в корнях, но в данном случае   особенно интересуют частное решение,  имеющее мнимые  корни:

$$ p_1 = \frac{-a_1}{a_0}, \quad p_{2,3} = \pm\sqrt{\frac{-a_2}{a_0}} = \pm j \sqrt{\frac{a_2}{a_0}} \tag{5}\label{5}$$

Поочерёдно интегрируя выражение для корней:

1.1. \( p_1 = \frac{\mathrm{d}z}{\mathrm{d}x} = \frac{a_1}{a_0} \quad \int{\frac{\mathrm{d}z}{\mathrm{d}x}} = \int{\frac{-a_1}{a_0}} \) или \(\mathrm{d}z = \int{\frac{-a_1}{a_0}\mathrm{d}x} \) получаем выражение для описания кривизны деформированного пространства в области прилегающей к массе вещества.

$$z_1 = A \, e^{-p_1x} = Ae^{-\frac{a_1}{a_0}x} \tag{6}\label{6}$$

Здесь:

• \(А\)- постоянная интегрирования, определяется из начальных условий.
• \(x = \mathbf{l} =4\frac{a_0}{a_1} – характерная длина на котором прогиб  на рассматриваемом участке можно считать приблизительно равным нулю.

1.2. \(p_{2,3} = \frac{\mathrm{d}z}{\mathrm{d}x} = \sqrt{-\frac{a_2}{a_0}} \quad \int{\frac{\mathrm{d}z}{\mathrm{d}x}} = \int{\sqrt{-\frac{a_2}{a_0}}}\)

Общий интеграл этого уравнения имеет вид:

$$z = B \sin{\sqrt{\frac{a_2}{a_0}}} x + C \cos{\sqrt{\frac{a_2}{a_0}}}x \tag{7}\label{7} $$

Здесь \(В\) и \(С\) – постоянные интегрирования, определяемые из начальных условий.

Условия на границах прогиба в пространстве, прилегающем к массе вещества  дают два  уравнения:

В центре массы \(М\):

$$\begin{align}
\text{при} \, x = 0 \quad \text{прогиб} \, \mathbf{z=0} \\
\text{при} \, x \geq \mathbf{l} = \frac{4a_1x_1}{a_0} \to \inf \quad \text{прогиб} \, \mathbf{z=0}
\end{align}$$

Из первого условия следует (так как \(\sin{\sqrt{\frac{a_2}{a_0}}}x = 0\) и \(\cos{\sqrt{\frac{a_2}{a_0}}}x = 1\)):

$$ 0 = C \tag{8}\label{8} $$

Таким образом, прогиб  пространства, прилегающего к массе вещества, описывается синусоидой с уравнением:

$$z=B\sin{\sqrt{\frac{a_2}{a_0}}}x \tag{9}\label{9}$$

Применяя второе условие, подставляем в это уравнение прогиб \(z=0\) и \(x = l\) получаем:

$$ 0 = B\sin{\sqrt{\frac{a_2}{a_0}}}l \tag{10}\label{10}$$

Отсюда следует, что или \(В\) или \(\sqrt{\frac{a_2}{a_0}}l\) равны нулю.

Если  \(В\)  равно нулю, то из уравнения \(\eqref{9}\) следует , что прогиб в на любом участке прилегающей к массе \(М\) равен нулю, то есть пространство остается не деформированным, это противоречит имеющимся данным по искривлению пространства времени,  достоверно проверенных  в ОТО  для других объектов, но не для Солнечной системы. Следовательно, \(\sin{\sqrt{\frac{a_2}{a_0}}}l \), и величина \(\sqrt{\frac{a_2}{a_0}}l\) может принимать следующий бесконечный ряд значений:

$$ x = \sqrt{\frac{a_2}{a_0}}l = 0, \, \pi, \, 2\pi, \, 3\pi, \, \ldots, \, n\pi $$

где \(n\) – любое целое число,  \(n=1\) -формирует основную гармонику прогиба.

Отсюда следует, что \(n\pi = \sqrt{\frac{a_2}{a_0}}l\), а так как \(\sqrt{\frac{a_2}{a_0}} = \sqrt{\frac{F}{GMm}}\), то  в зависимости от кривизны пространства будут изменяться по следующей зависимости либо:

• сила гравитационного  взаимодействия   при других неизменных  значениях  физических величин
  $$ F = \frac{n^2\pi^2GMm}{R^2} \tag{11}\label{11}$$
• либо радиусы орбит  при тех же  дополнительных условиях:
  $$ R = n\pi\sqrt{\frac{GMm}{F}} \tag{12}\label{12}$$
• либо гравитационная постоянная, будет соответствовать по величине (на характерных расстояниях для различной постоянной кривизны) значениям  электрической  постоянной  для закона О.Кулона, или постоянной ядерного взаимодействия и т.д.
  $$G=\frac{FR^2}{Mmn^2\pi^2}\tag{13}\label{13}$$

Подводя итог изложенному  расчету прогибов пространства  Солнечной системе можно сделать вывод о том, что его величина определяется суммарной величиной имеющей монотонно затухающую (возрастающую)  и периодическую составляющие согласно сводного выражения по прогибам пространства:

$$ Z = A \, e^{-\left[\frac{m}{t^2}\frac{R^2}{GMm}\right]x}+B\sin{n\pi\sqrt{\frac{F}{GMm}}}x \tag{14}\label{14}$$

Наличие  множителя \(n\) соответствует появлению дольных ( кратных значений) постоянных прогиба и которые также вносят свой вклад (иногда значительный) в суммарную кривизну участка пространства, прилегающего к веществу.

Обоснование необходимости наличия усложненных дифференциальных уравнений для более точного описания гравитационного взаимодействия и их связь с классической формой закона всемирного тяготения

Наличие периодической составляющей по прогибу пространства может свидетельствовать о наличии противодействия, в виде упругости деформируемого пространства, прилегающего к массе вещества. Такую возможность  теоретически подтверждает приведенное выше дифференциальное уравнение, со следующим членом, размерность коэффициента при  очередной производной должна быть либо давлением – \(Р\) , либо размерностью  модуля упругости пространства – \(Е\) или размерностью текущих значений модуля упругости – нормальных напряжений \(\left[\sigma_{H}\right]\) в сечениях деформированного пространства.

$$\begin{equation}
G \\ [L^3M^{-1}T^{-2}]
\tag{15a}\label{15a}
\end{equation}$$

$$\begin{equation}
R^2 \\ [L^2M^0T^0] \tag{15b}\label{15b} \end{equation}$$

$$\begin{equation} F \\ [L^1M^1T^{-1}] \tag{15c}\label{15c} \end{equation}$$

$$\begin{equation} Mm \\ [L^0M^2T^0] \tag{15d}\label{15d} \end{equation}$$

$$\begin{equation} E \, \text{или} \, \left[\sigma_{H}\right] \\ [L^{-1}M^1T^{-2}] \tag{15e}\label{15e} \end{equation}$$

Дифференциальное уравнение четвертого порядка производной  для  уточненного описания гравитационного взаимодействия,  построенное по выше изложенному способу имеет вид:

$$ G \, Mm \frac{\mathrm{d^2}z}{\mathrm{d}x^2} + \frac{m}{t^2}R^2 \frac{\mathrm{d}z}{\mathrm{d}x} + F z + \frac{m}{t^2} \int{z\mathrm{d}z} + E \int{z\mathrm{d}x^2} = 0 \tag{16}\label{16}$$

ОпределительГурвица, построенный на коэффициентах при производных уравнения четвертого порядка и формула уравнения, повторяющая классическую форму приводится ниже.

$$ \Delta = \begin{bmatrix} \frac{m}{t^2}R^2 & \frac{m}{t^2} & E \\ G\,Mm & F & \left[\sigma_{H}\right] \\ 0 & \frac{m}{t^2}R^2 & \frac{m}{t^2} \end{bmatrix} = \left(\frac{m}{t^2}\right)^2\left( R^2F – G\,Mm – R^4E\right) = 0 \tag{17}\label{17}$$

Далее, раскрывая определитель, получим:

$$\left(\frac{m}{t^2}\right)^2 (R^2F – G\,Mm – R^4E) = 0 \tag{17a}\label{17a}$$

Откуда:

$$F = \frac{G\,Mm+R^4E}{R^2} \tag{17b}\label{17b}$$

Для уравнения \(\eqref{17a}\) остается действительным условие \(\frac{m}{t^2}\gt0\)

Отличие классического закона от уточненного полученного заключается в наличии дополнительного члена \(R^4E\) – который, при  расчетах деформации стержней называют жесткостью стержня. При этом стержнем приходится считать гибкую, упругую линию  (радиус планеты) по которой осуществляется гравитационное взаимодействие масс вещества.  Величина,  равная произведению квадратов радиусов  (длины полудуги синусоиды прогиба) – \(R^4 = J\) в инженерных расчетах имеет собственное название момент инерции сечения области пространства. Для  описания гравитационного взаимодействия в Солнечной системе – эта величина  равна радиусу орбиты планеты взятому в четвертой степени.

Для получения аналитической зависимости при расчетах массы, силы или радиусов орбит. необходимо произвести почленное деление размерностей длины или массы у всех членов  уравнения с отрицательным знаком на размерности  члена с положительным знаком. Тогда формула для расчета масс планет в Солнечной системе  примет вид:

$$ m = \frac{2M}{\frac{J}{j} + \frac{j}{J}} \tag{18}\label{18}$$

Здесь:

• \(М\) и \(J\) – масса и момент инерции сечения наибольшей планеты системы,– Юпитера. В расчете принимаются их постоянные значения;
• \(m\) и \(j\) – текущие значения масс любой из остальных планет с моментом инерции сечения соответствующей планеты.

Жесткость и упругость часто соотносят с электромагнитным взаимодействием, как правило,  действующих внутри массы вещества (например между молекулами). Но аналогичный механизм, похоже имеет место и на расстояниях сравнимых с радиусами орбит и массами, равными массам планет. Уравнение \(\eqref{18}\) имеет физические величины, содержащие размерности пространственные и массовые, это обстоятельство означает, что оно описывает равновесное состояние системы “пространство-вещество’ и является уравнением статики. В технических расчетах, для  сравнительно малых расстояний (по сравнению с характерными для Солнечной системы размерами) имеется формула для расчета прогиба стержней, которой пользуются при расчетах механических конструкций. Математической моделью  которой послужила упругая линия. При  выполнении  расчетов кривизны – \(\frac{1}{\rho(x)}\),  под воздействием нагрузки \(P_k\) пользуются формулой, которая  имеет вид:

$$\frac{1}{\rho(x)} = \pm \frac{\frac{\mathrm{d^2}z}{\mathrm{d}x^2}} {\sqrt{\left[ 1 + \bigl(\frac{\mathrm{d}z}{\mathrm{d}x}\bigr)^2 \right]^3}} = P_k\frac{\left(\mu l\right)^2}{EJ} \tag{19}\label{19}$$

Здесь:

• \(P_k\) – минимальная сила, при которой прогиб стержня осуществляется по одной полуволне основной гармоники;
• \(E\) – модуль упругости пространства в котором проходит линия взаимодействия масс планет;
• \(J\) – момент инерции сечения области деформации  для упругой линии. Для механической конструкции в виде гибкого стержня равна произведению поперечного сечения стерня на квадрат расстояния от точки закрепления;
• \(l\) – полная длина участка пространства (волны прогиба) на котором осуществлен прогиб стержня;
• \(\mu\) – коэффициент, учитывающий вид закрепления концов синусоиды прогиба. Различают следующие виды закрепления концов:
  • шарнирно опертые концы – весь участок стержня участвует в деформациях, для  такого вида закрепления  концов стержня \(\mu = 1\);
  • защемленные – в прогибе участвует только половина участка деформации, для  такого вида закрепления концов стержня \(\mu = 0,5\);
  • один конец стержня защемлен, второй – шарнирно оперт, то есть промежуточный вариант деформации, для него \(\mu = 0,7\).

В практических расчетах  стержней на устойчивость и  величину прогиба рассматривают:

$$\sqrt{\left[ 1 + \bigl(\frac{\mathrm{d}z}{\mathrm{d}x}\bigr)^2\right]^3} \sim 1$$

Так как величина \(\frac{\mathrm{d}z}{\mathrm{d}x}\) обычно очень мала и все выражение очень мало отличается от 1. При этом  окончательный вид формулы становится:

$$E\,J\frac{\mathrm{d}^2z}{\mathrm{d}x^2} + \frac{m}{t^2}(\mu l)^2\frac{\mathrm{d}z}{\mathrm{d}x} + P_k z + \frac{m}{t^2}\int{z\mathrm{d}x} = 0 \tag{20}\label{20}$$

Для практического использования формула расчета стержней на устойчивость  была представлена Л. Эйлером в 1744 году в виде неполного уравнения второго порядка производной, которая представлена ниже:

$$ E \, J \frac{\mathrm{d^2}z}{\mathrm{d}x^2} = – P_k z \tag{20a}\label{20a} $$

Им же были найдены решения уравнения в общем случае.  Определены   формы прогиба стержня в функции от способа закрепления концов стержней. Произведены расчеты постоянных интегрирования (на основе которых сделаны представленные  выше аналогичные расчеты для дифференциальной формы  уравнения ЗВТ). Проделаны также  другие исследования условий устойчивости   стержней (в том числе с учетом  гибкости стержней).                      

Сравнение обеих формул: дифференциальной   для ЗВТ и формулы  составленной на основе уравнения Л. Эйлера показывают их практическое совпадение. И поскольку остается неотмененным ещё один закон И. Ньютона, требующий равенства противодействующих сил, то при некоторых условиях будет соблюдаться равенство различных по своей физической природе сил, т.е. :

$$ G \, Mm = EJ \tag{21}\label{21}$$

Как показывает совместное  решение  обоих уравнений,  такое равенство соблюдается для  планеты Юпитер. Поскольку все числовые значения физических величины , задействованные в уравнении \(\eqref{21}\)  известны, за исключением числового значения модуля упругости пространства, то можно определить и его числовое значение:

$$E = \frac{G \, Mm}{J} = \frac{6,672E – 11 \ast 1,99E +30 \ast 1,90E+27}{3,66E+47} = 6,78E-01 \, м^{-1} \, кг \, с^{-2}$$

Здесь:

• \(G = 0,672E-11 \, м^3 \, кг \, с^{-2} \) – гравитационная постоянная;
• \(M=1,99E+30 \, кг\) – масса Солнца;
• \(m=1,90E+27 \, кг\) – масса Юпитера;
• \(J = R^4= 3,66E+47 \, м^4\)  – момент инерции сечения.

На расстояниях, соизмеримых  с характерными размерами Солнечной системы, наиболее реально ожидать одновременного наличия гравитационных и электромагнитных сил. Электромагнитному взаимодействию  для  отдельных частичек вещества (молекул) обычно соотносят силы упругого взаимодействия. И только внутри пространства занимаемого массами Солнца и планет, могут проявиться ядерные силы.

Расчет волн прогиба внутри тяготеющих масс  необходим при расчетах, направленных на описание внутреннего строения планет и Солнца, а так же может  использоваться в космогонических моделях описания внутреннего строения  Вселенной. При этом, для составления уточненного дифференциального уравнения необходимо  особую роль уделить еще одной физической величине \(\rho\) – плотности вещества. Но размерность \([\rho] = [L^{-3}M^1]\),  недостаточна для представления её коэффициентом при дополнительной производной.

Для того, чтобы размерность дополнительного члена дифференциального уравнения стала равной размерностям остальных членов, необходимо ввести дополнительно величину \(\gamma\) – удельный вес вещества в деформируемом объеме пространства – \(V^2\), то есть ввести ускорение \(g\) с размерностью \([L^1M^0T^{-2}]\), а произведение  ускорения и удельной плотности \([g\rho] = \gamma\) – удельному весу вещества. Имеющего размерность \([L^{-2}M^1T^{-2}]\).

При таких оговорках пятый член дифференциального уравнения для описания гравитационного взаимодействия принимает вид:  

$$ G \, Mm \frac{\mathrm{d^2}z}{\mathrm{d}x^2} + \frac{m}{t^2}R^2\frac{\mathrm{d}z}{\mathrm{d}x} + F \, z + \frac{m}{t^2}\int{z}{\mathrm{d}x} + E \int{z\mathrm{d}x^2} + \gamma \int{z\mathrm{d}x^3} = 0 \tag{22}\label{22}$$

Или еще одна удобная форма:

$$\gamma V^2 \frac{\mathrm{d^3}z}{\mathrm{d}x^3} + G \, Mm \frac{\mathrm{d^2}z}{\mathrm{d}x^2} + \frac{m}{t^2}R^2\frac{\mathrm{d}z}{\mathrm{d}x} + Fz + \frac{m}{t^2} \int{z\mathrm{d}x} + E \int{z\mathrm{d}x^2} = 0 \tag{22a}\label{22a}$$

Здесь:

• \(\frac{m}{t^2}\) -дополнительный множитель , введенный ранее для коэффициентов при производных для нечетных членов уравнения присутствует в неявном виде;
• \(\gamma\) – удельный вес вещества,  имеет размерность – \([L^{-2}M^{1}T^{-2}]\);
• \(V^2\) – объем, в котором гравитационные силы деформируют пространство.

Для приведения дифференциальной формы уравнения к классической на коэффициентах при производных построим определитель Раусса-Гурвица и раскроем его. Для сокращения записи она будет произведена для характеристического уравнения:

$$ a_0p^5 + a_1p^4 + a_2p^3 + a_3p^2 + a_4p + a_5 = 0 \tag{23}\label{23} $$

Здесь:

• \(a_0 = G \, Mm\)
• \(a_1 = \frac{m}{t^2}R^2\)
• \(a_2 = F\)
• \(a_3 = \frac{m}{t^2}\)
• \(a_4 = E\)
• \(a_5 = \gamma\)
• \(p = \frac{\mathrm{d}z}{\mathrm{d}x}\)
• \(\frac{1}{p} = \int{z\mathrm{d}x}\)
• \(a_0 \gt 0, \, a_1 \gt 0, \, a_2 \gt 0, \, a_3 \gt 0, \, a_4 \gt 0, \, a_5 \gt 0\)

Главный определитель:

$$ \Delta_5 = \begin{bmatrix}
a_1 & a_3 & a_5 & 0 & 0 \\
a_0 & a_2 & a_4 & 0 & 0 \\
0 & a_1 & a_3 & a_5 & 0 \\
0 & a_0 & a_2 & a_4 & 0 \\
0 & 0 & a_1 & a_3 & a_5
\end{bmatrix} \tag{24}\label{24}$$

Диагональные миноры:

$$ \begin{align*}
\Delta_4 = \begin{bmatrix}
a_1 & a_3 & a_5 & 0 \\
a_0 & a_2 & a_4 & 0 \\
0 & a_1 & a_3 & a_5 \\
0 & a_0 & a_2 & a_4
\end{bmatrix} = (a_1a_2 – a_0a_3)(a_3a_4 – a_2a_5) – (a_1a_4 – a_0a_5)^2 = \Delta_2(a_3a_4 – a_2a_5) – (a_1a_4 – a_0a_5)^2 \gt 0 \\

\Delta_3 = \begin{bmatrix}
a_1 & a_3 & a_5 \\
a_0 & a_2 & a_4 \\
0 & a_1 & a_3 \\
\end{bmatrix} = a_3(a_1a_2- a_0a_3) – a_1(a_1a_4 – a_0a_5) = a_3 \Delta_2 – a_1(a_1a_4 – a_0a_5) \gt 0 \\

\Delta_2 = \begin{bmatrix}
a_1 & a_3 \\
a_0 & a_2
\end{bmatrix} = (a_1a_2- a_0a_3) \gt 0

\end{align*} \tag{24a}\label{24a}$$

Сопоставление  результатов раскрытия определителей уравнений третьего, четвертого пятого порядка производной показывает, что аналитическая запись уравнений баланса  базируется  на соблюдении следующих условий:

• классический вид ЗВТ (полученного,  из дифференциального уравнения  третьего порядка производной):
  $$ (a_1a_2-a_0a_3) = 0 \tag{25a}\label{25a}$$
  $$R^2\frac{m}{t^2}F – GMm\frac{m}{t^2} = 0 \tag{25b}\label{25b}$$
  при: \(\frac{m}{t^2} \gt 0\) и \((FR^2 – GMm) = 0\)
• уточненный вид (полученного,  из дифференциального уравнения  четвертого порядка производной):
  $$(a_1a_2 – a_0a_3)a_3 – a_4a_1^2 = 0 \tag{26a}\label{26a}$$
  $$\bigl(\frac{m}{t^2}\bigr)^2(R^2F – G Mm) – ER^4\bigl(\frac{m}{t^2}\bigr)^2 = 0 \tag{26b}\label{26b}$$
  при: \(\bigl(\frac{m}{t^2}\bigr)^2 \gt 0\), \((FR^2 – GMm) \gt 0\) и \(R^2F – GMm – ER^4 = 0\)
  

***** Необходимо отредактировать участок <НАЧАЛО Участка> *****

Первый вариант справедлив для описания гравитационного взаимодействия для области пространства где

На

В направлении  взаимодействующей массы m прилегающего к этим массам вещества.

***** Необходимо отредактировать участок <КОНЕЦ Участка> *****

В инженерной практике расчёт на устойчивость стержня (механической модели упругой линии) производится по дифференциальному уравнению предложенному и детально исследованному Л. Эйлером в 1744г. В частности кривизна этой линии описывается уравнением:

$$\frac{1}{\rho(x)} = \pm \frac{\frac{\mathrm{d^2}z}{\mathrm{d}x^2}}{\sqrt{\left[1+ \bigl(\frac{\mathrm{d}z}{\mathrm{d}x}\bigr)^2\right]^3}} = \frac{P_kz}{EJ} \tag{27}\label{27}$$

Здесь: 

• \(z(x,y) = \frac{1}{\rho(x)}\) – текущее значение кривизны пространства  в точке  \(х\)  или \(у\)  по  радиусу орбиты планеты  при допущении, что радиус планеты является  упругой линией. Ось \(z\) – нормальна  к плоскости  \(х у\).

Обычно в расчётах  на устойчивость упругих стержней пренебрегают следующей величиной по причине малости её отличия по сравнению с 1:

$$\sqrt{\left[1+ \bigl(\frac{\mathrm{d}z}{\mathrm{d}x}\bigr)^2\right]^3} \tag{27a}\label{27a}$$

Установлено, что устойчивость изогнутых стержней,  по воздействием нагрузки. составляет величину порядка 2-3% от длины  стержня (в данном случае радиуса орбиты планеты), то есть величиной    обычно пренебрегают и  решают уравнение  для прогибов стержня) (упругой линии) по формуле Л. Эйлера для величины критической (минимальной) силы при которой стержень теряет устойчивость  (разрушается)  и которая  имеет вид:

$$ EJ\frac{\mathrm{d^2}z}{\mathrm{d}x^2} = P_kz \tag{27b}\label{27b}$$

Тогда величина кривизны,  при которой устойчивость стержня сохранится:

$$\frac{\mathrm{d^2}z}{\mathrm{d}x^2} = \frac{P_kz}{EJ} \quad \text{или} \quad EJ\frac{\mathrm{d^2}z}{\mathrm{d}x^2} = – P_kz \tag{28}\label{28}$$

Здесь:

• \(EJ\) – жесткость упругой линии (пространства по радиусу от Солнца до планеты)
• \(E\) – модуль упругости пространства . Его текущее значение по радиусу \([\sigma_H]\), то есть \([\sigma_H] \leq E\) называют нормальными  напряжениями, возникающими в перпендикулярном  сечении области деформации в направлении по (упругой линии)  – радиусу взаимодействия  между массами тел
• \(J\) – момент инерции сечения  деформированного пространства, прилегающего к  массам тел.

Решение уравнения относительно производной (по прогибу)  имеет вид:

$$Z = B\sin{\sqrt{\frac{-P_k}{EJ}x}} \tag{29}\label{29}$$

Здесь:

• \(B\) – постоянная интегрирования, определяемая из начальных условий.
• \(p_{1,2} = \pm j \sqrt{\frac{P_k}{EJ}}\) – корни уравнения \(\eqref{28}\)

Но аналитический вид решения по величине длины волны прогиба  (формула \(\eqref{29}\) ), свидетельствует о возможности искривления пространства вблизи одиночной массы или между двумя массами по затухающей волнообразной прямой.

Например, при движении планет по своим орбитам  в Солнечной  системе, они иногда занимают относительно друг друга положения, при котором гравитационные силы,  действующие на каждую из планет со стороны  Солнца, складываются (явление, получившее название “парада  планет”) соответствует нахождению всех, или значительной части планет, на одной линии. Суммарное  гравитационное притяжение искривляет пространство по нескольким полуволнам с уменьшающейся длиной  волны. Дальнейшее движение планет приводит к более равномерному их распределению вокруг Солнца, и,  должно бы было привести к скачкообразному возвращению длины волны прогиба к основной гармонике, так как  каждая из временно образовавшихся полуволн прогиба не закреплена массой вещества. Но этого реально не  происходит, так как фактические массы планет значительно больше тех, которые необходимы для закрепления полуволны прогиба пространства по основной гармонике. Поэтому пространство, многократно изогнутое по нескольким затухающим  полуволнам прогиб, стабильно остаётся в таком состоянии из-за инертности массы вещества в несколько раз, превышающей значение, необходимое для удержания прогиба по волне основной гармоники.

Графическое решение дифференциального уравнения подтверждает аналитическое и позволяет наглядно рассмотреть форму прогиба пространства. Необходимые графические построения  приведены на рис 1. с примечаниями.

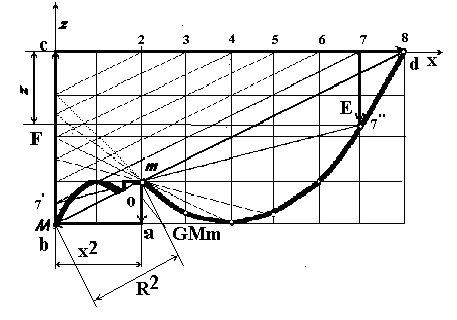
В качестве аналога графического решения дифференциального уравнения использована прямоугольная спираль (полиортогон) с октавным соотношением смежных сторон (ортогонов – коэффициентов при производных). Концы полиортогона соединены диагональю. Сечение пространства по продольной координате \(х\), (например между Солнцем и Плутоном) в плоскости эклиптики поделено на восемь участков. Через границы участков проведены прямые, одна диагонали параллельная полиортогону (\(Md\)), вторая – перпендикулярно плоскости эклиптики (77”). Точка пересечения (7’) вспомогательной прямой (77’), через полюс полиортогона (точка m) соединена с точкой (7”). В соответствии с рядом коэффициентов при производных физических величин отрезок полиортогона (77”) должен иметь размерность нормальных напряжений возникающих в деформированном пространстве, а их предельное значение – соответствовать модулю упругости пространства (на рисунке отрезок – 44”).

Примечание. На рис 1 представлены построения профиля прогиба пространства  Солнцем и Сатурном. Если, на линии взаимодействия Солнца и Сатурна в рассматриваемый момент времени планет нет, то профиль прогиба пространства вне взаимодействующих тел будет описываться кривой \(mEd\), а профиль прогиба пространства между Солнцем и Сатурном по кривой \(Mm\). Для некоторых планет период синусоиды прогиба укорочен на 0,75-0,7 от максимального- равного радиусу орбиты за счёт эффекта защемления. И только для трёх планет: Земли, Юпитера и Сатурна, шарнирно опертые концы синусоиды прогиба обеспечивают равенство радиуса  орбиты и синусоиды прогиба.

Появление в формуле модуля упругости, фактически означает то,  что силе гравитации противодействует равная ей сила упругости, которая по существующим представлениям обязана своим существованием электромагнитному взаимодействию.  Для  нагруженного и изогнутого стержня Л.Эйлером было предложено дифференциальное уравнение, для величины силы, при которой изогнутый стержень еще не разрушается. Это уравнение, решенное через коэффициенты при производных,  имеет вид:

$$P_k = \frac{EJ}{(\mu l)^2} \tag{30}\label{30}$$

 Здесь:

• \(E\) – модуль упругости материала стержня (в данном случае пространства),
• \(J\) –  момент инерции сечения, равный произведению квадрата расстояния от начала координат до сечения,  так же имеющего размерность площади,
• \(\mu l\) – приведённая длина стержня (в данном случае  длина геодезической прямой, соединяющей взаимодействующие массы вещества).  По Л. Эйлеру \(\mu\) принимает значения: 
  • 0,5- для двух защемлённых концов; 
  • 1- для двух шарнирно опёртых концов;
  • 2-для одного защемлённого и одного шарнирно опёртого.

Дифференциальная форма по Л. Эйлеру представляет собой неполное уравнение второго порядка производной и имеет вид:

$$EJ\frac{\mathrm{d^2}z}{\mathrm{d}x^2} + P_k z = 0 \tag{31}\label{31}$$

$$EJ\frac{\mathrm{d^2}z}{\mathrm{d}x^2} + \frac{m}{t^2}(\mu l)^2 \frac{\mathrm{d}z}{\mathrm{d}x} + P_k z + \frac{m}{t^2} \int{z\mathrm{d}x} = 0 \tag{31a}\label{31a}$$

Уравнение \(\eqref{31a}\) – является полным дифференциальным уравнением третьего порядка производной. Уравнение Л. Эйлера \(\eqref{31}\) – является  частным случаем от общего решения и включает в себя только чётные члены уравнения.  От дифференциальной формы ЗВТ приведённое уравнение отличается только физическими величинами первых членов уравнения и направлением   действия силы, противодействующей гравитационной сжимающей силе. Определитель Раусса-Гурвица построенный на коэффициентах при производных даёт при раскрытии классический вид уравнения для критической силы, полученный Л. Эйлером.

Наличие в Солнечной системе девяти планет и одной звезды, говорит о том, что уравнение (или система уравнений) в корнях должно давать десять значений масс и десять синусоид прогиба пространства, отличающихся по амплитуде и периоду.

Как видно из приведённых рассуждений, два из требуемых уравнений уже имеются. За орбитой Сатурна, на  участке расположения планет гигантов  до Плутона безраздельно действует сжимающая – гравитационная сила. Прогиб описывается синусоидальной кривой с одним защемлённым (в недеформированном пространстве) и одним шарнирно опертым концом (на массе Солнца). 

На участке планет земной группы от Меркурия до Земли действуют две силы – сжимающая (гравитационная) и противодействующая ей сила упругости. Прогиб описывается синусоидальной кривой с одним шарнирно опертым (на массе планеты) и одним защемлённым концом (на массе Солнца).

На небольшом участке пространства от Земли до Сатурна эти силы примерно равны. Пространство на этом участке деформируется по кривой близкой к синусоиде с шарнирно опертыми концами. Шарнирно опертые концы располагаются на массе Солнца и массах планет: Земли. Юпитера, Сатурна.

На двух участках околосолнечного пространства  у Марса  и Нептуна гравитационная и сила упругости примерно равны. Периоды и амплитуды синусоиды прогиба уменьшаются вдвое. Направление прогиба при этом  противоположны, а концы синусоиды жестко защемлены.

На пространстве,  прилегающем к Солнцу,  действуют две не равные силы: большая гравитационного сжатия и меньшая сила упругости. Что вызывает монотонное затухание прогиба пространства (от гравитационной силы)  с небольшой периодической составляющей затухания (от силы упругости). Концы синусоиды прогиба жестко защемлены в окружающем недеформированном пространстве.

Приведённые рассуждения, указывают на особую роль волновых процессов, реализующихся на синусоидальных и производных от синусоидальных форм прогиба пространства. Которые получаются фиктивным уменьшением (за счёт участка на котором  происходит защемление) уменьшением периода и амплитуды прогиба). 

Правильность соответствия физической картины деформации пространства, полученной на основе полученного решения, подтверждается  расчётом масс планет в Солнечной системе. Расчётная формула, получена на основе уравнения чётвёртого порядка производной. Она имеет вид:

$$m = \frac{2M_k}{\frac{j_n}{J_k} + \frac{J_k}{j_n}} \tag{32}\label{32}$$

Здесь:

• \(m\) – текущее  значение величины массы планет;
• \(2 M_k\)  – масса наибольшей    планеты – Юпитера;
• \(J_k\) – момент инерции  сечения для наибольшей планеты, равный   расстоянию до Солнца  в четвёртой степени;
• \(j_n\) – момент инерции сечения  каждой из  \(n\) – планет, также равный расстоянию планеты до Солнца  в четвёртой степени.

Примечание: Массы вещества, полученные в результате расчёта по данной формуле, соответствуют радиусам планет для основной гармоники прогиба,  имеющей форму синусоиды с шарнирно опёртыми концами на массах планет. Эти данные приведены в таблице 1.

Таблица 1. РАСЧЁТ МАСС ПЛАНЕТ СОЛНЕЧНОЙ СИСТЕМЫ
(вариант с шарнирно опертыми концами синусоиды прогиба)

Название планеты	Расстояние до Солнца (м.) -\(r\)	Момент инерции сечения области деформации,           (\(м^4\)) – \(J\)	Отношение моментов инерции сечения области деформации планеты   к моменту инерции сечения Юпитера – \(\frac{j}{J}\)	Обратное отношение момента инерции сечения области деформации планеты – \(\frac{J}{j}\)	Сумма прямого и обратного отношений моментов инерции сечений – \(\frac{j}{J}+\frac{J}{j}\)	Текущее расчетное значение массы планеты (кг) – \(m=\frac{2M}{\frac{j}{J}+\frac{J}{j}}\)	Фактическое значение массы планеты (кг)
Меркурий	5,79E+10	1,12E+43	3,06E-05	3,26E+04	3,26E+04	1,15E+23	3,11E+23
Венера	1,08E+11	1,37E+44	3,74E-04	2,68E+03	2,68E+03	1,40E+24	4,79E+24
Земля	1,50E+11	5,01E+44	1,37E-03	7,33E+02	7,33E+02	5,10E+24	5,88E+24
Марс	2,28E+11	2,70E+45	7,35E-03	1,36E+02	1,36E+02	2,75E+25	6,29E+23
Юпитер	7,78E+11	3,67E+47	1	1	2	1,87E+27	1,87E+27
Сатурн	1,43E+12	4,16E+48	1,13E+01	8,82E-02	1,14E+01	3,27E+26	5,60E+26
Уран	2,87E+12	6,80E+49	1,85E+02	5,39E-03	1,85E+02	2,02E+25	8,55E+25
Нептун	4,50E+12	4,09E+50	1,12E+03	8,96E-04	1,12E+03	3,35E+24	1,01E+26
Плутон	5,91E+12	1,22E+51	3,32E+03	3,01E-04	3,32E+03	1,12E+24	5,29E+24

Получено соответствие расчётных масс вещества с их реальными значениями.

Значения масс планет могут быть существенно уточнены, если применить понятие «защемления» концов синусоиды прогиба. Это понятие введено Л. Эйлером для описания прогиба стержневых конструкций. Стержнем в рассматриваемом случае служит геодезическая прямая, соединяющая центры масс планет. При таком допущении, прогиб линии может осуществляться только на части синусоиды.

Из курса «Сопротивления материалов» известно, что для стержневых конструкций защемление с одной стороны синусоиды прогиба эквивалентно укорочению синусоиды прогиба до величины, равной 0,7 первоначальной длины, а защемление обеих сторон синусоиды прогиба, укорочению длины волны равной 0,5 от первоначальной длины полуволны прогиба.

В графическом решении для прогиба пространства, приведенном на рис 1., защемлению соответствует участок пространства в виде головки и воротничка шахматной пешки. Участок пространства где полуволна прогиба укорачивается для участка пространства деформированного планетами гигантами (юбка шахматной пешки укорочена за счёт участка на абрис головки пешки).

В приведённой формуле \(\eqref{32}\), области защемления для планет гигантов соответствует критическое значение момента инерции сечения – \(J_k=R^4\) Юпитера, равного радиусу орбиты Юпитера, взятому в четвёртой степени.

Планеты между Юпитером и не возмущенным пространством, один конец защемленный конец синусоиды прогиба будут иметь в пространстве прилегающем к Юпитеру, а второй конец- шарнирно опертым в не возмущенном пространстве.

Планеты, расположенные между Солнцем и Юпитером, защемлённый один конец синусоиды прогиба имеют в массе Солнца, а шарнирно опертый конец синусоиды на массе Юпитера. На участках расположения планет земной группы и участке расположения планет гигантов прогибы пространства имеют различные направления прогиба. На месте изменения направления прогиба находится планеты Земля и Сатурн, для которых синусоиды прогиба имеет шарнирно опертые концы.

Две планеты, находящаяся на участке пространства с изменением направления прогиба на противоположное, будут иметь два защемлённых конца и коэффициент укорочения радиуса до 0,5 фактического радиуса что будет соответствовать эффекту защемления обеих концов синусоиды прогиба. Одновременные изменения величины участка защемления на синусоиде прогиба приводит к тому что для планет земной группы синусоида прогиба удлиняется, за счёт укорочения синусоиды прогиба для планет гигантов. Относительное удлинение приведённого радиуса орбиты планеты- μ, меняется на величину от 1/(0,75- 0,8675) до 0,75 фактического радиуса орбиты.

В таблице 2 приведены расчётные данные, учитывающие удлинение и укорочения радиусов орбит для планет Солнечной системы, вызванные защемлением концов синусоиды прогиба. По данным таблицы построен графики. На рис 2 показывается деформации пространства и закрепление дуг прогиба. Отчётливо видна зависимость изменения поправочных коэффициентов для радиусов орбит планет. На участке планет земной группы для правильности расчёта необходимо формально удлинять орбиты в 1/0,7 раз, а на участке планет гигантов, укорачивать в 0,7 раза.

Таблица 2. УТОЧНЁННЫЙ РАСЧЁТ МАСС ПЛАНЕТ СОЛНЕЧНОЙ СИСТЕМЫ (с учётом защемления концов синусоиды прогиба)

Название планеты	Расстояние до Солнца (м.) – \(r\)	Коэффициент \(\mu\) учитывающий характер закрепления концов полуволны прогиба, в виде защемления концов (одного или двух) или отсутствие защемления, то есть шарнирно опертые по Эйлеру	Фактический коэффициент \(\mu\) , учитывающий характер закрепления концов полуволны прогиба, в виде защемления концов (одного или двух) или отсутствие защемления, то есть шарнирно опертые	Расстояние до Солнца (м.) – \(r\)  с учётом уменьшения   величины  радиуса за счёт эффекта защемления	Момент инерции сечения области деформации,           \((м^4) – J\)	Отношение моментов инерции сечения области деформации планеты   к моменту инерции сечения Юпитера – \(\frac{j}{J}\)	Обратное отношение момента инерции сечения области деформации планеты – \(\frac{J}{j}\)	Сумма прямого и обратного отношений моментов инерции сечений – \(\frac{j}{J}+\frac{J}{j}\)	Текущее расчетное значение массы планеты (кг) – \(m=\frac{2M}  {\frac{j}{J}+\frac{J}{j}}\) . С учётом защемления – укорочение и удлинение радиуса орбиты	Значение массы планет, рассчитанной по аналогу упрощенной формулы Клосса (шарнирно-опертые концы прогиба \(\mu=1\))	Фактическое значение массы планеты (кг)
1	2	3	4	5	6	7	8	9	10	11	12
Меркурий	5,79E+10	1/0,7	1,28	3,02E+43	3,04E+43	8,24E-05	1,21E+04	1,21E+04	3,08E+23	1,15E+23	3,11E+23
Венера	1,08E+11	1/0,7	1,36	4,62E+44	4,69E+44	1,26E-03	7,93E+02	7,93E+02	4,72E+24	1,39E+24	4,79E+24
Земля	1,50E+11	1	1,03	5,70E+44	5,75E+44	1,56E-03	6,42E+02	6,42E+02	5,82E+24	5,17E+24	5,88E+24
Марс	2,28E+11	0,5	0,39	6,19E+43	6,19E+43	1,69E-04	5,91E+03	5,91E+03	6,32E+23	2,76E+25	6,29E+23
Юпитер	7,78E+11	1,0	1,00	3,66E+47	3,66E+47	1,00E+00	9,99E-01	2,00E+00	1,87E+27	1,87E+27	1,87E+27
Сатурн	1,43E+12	1,0	0,87	2,40E+48	2,39E+48	6,55E+00	1,53E-01	6,70E+00	5,58E+26	3,25E+26	5,60E+26
Уран	2,87E+12	0,7	0,70	1,63E+49	1,60E+49	4,45E+01	2,25E-02	4,45E+01	8,40E+25	2,02E+25	8,55E+25
Нептун	4,50E+12	0,5	0,43	1,34E+49	1,35E+49	3,66E+01	2,74E-02	3,66E+01	1,02E+26	3,34E+24	1,01E+26
Плутон	5,91E+12	0,7	0,68	2,59E+50	2,59E+50	7,09E+02	1,41E-03	7,09E+02	5,28E+24	1,12E+24	5,29E+24

Выводы

Таким образом, дифференциальная форма закона всемирного тяготения:

• подтверждает правильность описания  реальной картины гравитационного взаимодействия, учитывающей деформации пространства под воздействием слабых и сильных гравитационных полей. При этом эффекты, связанные с действием слабых полей куда более масштабны и более легки для  экспериментальной проверки, по сравнению с эффектами кривизны пространства в сильных гравитационных полях;

• объединила в единое целое два подхода на гравитационное взаимодействие  по ЗВТ и ОТО;

• дала возможность уточнить физическую картину гравитационного взаимодействия;

• получила математическое описание прогибов пространства на базе традиционного дифференциального исчисления;
• дала возможность рассчитать радиусы планет Солнечной системы и дать объяснение существующей эмпирической формулы для  подсчёта радиусов планет;

• на основе уточнённой формулы для описания гравитационного взаимодействия и фактических числовых значений для радиусов орбит позволила рассчитать значения масс планет в Солнечной системе;

• дала принципиально новую основу для описания процесса образования планет в том числе и Земли.

Список литературы

1. Мэрион, Дж. Б. Физика и физический мир. – М.,1975.

2. Большая советская энциклопедия : в 30 т. – 3-е изд. – М., 1972

3. Фатеев, Ф.В. Основы линейной теории автоматического регулирования. – М.Л.: Госэнергоиздат, 1954

4. Корн, Г. Справочник по математике / Г. Корн, Т. Корн. – М.: Наука, 1984